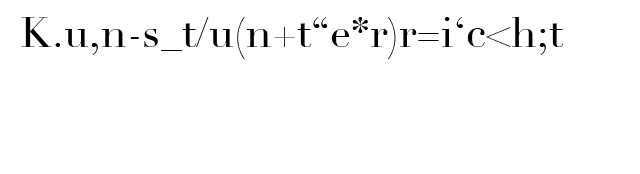Parallelprojektion kurz und knapp

Die Parallelprojektion (Axonometrie, umgangssprachlich auch Parallelperspektive) erlaubt eine einfache und übersichtliche Darstellung des dreidimensionalen Raumes in einer Bildfläche. Im Gegensatz zur Fluchtpunktperspektive wirkt sie weniger wirklichkeitsnahe aber sachlicher. Sie eignet sich zur Entwicklung, Planung und sachlichen Vermittlung von Architekturen, Möbel, Fahrzeugen und anderen Produkten. Im Folgenden wird eine knappe Zusammenstellung weniger Typen gemacht. Für Ausführungen siehe Parallelprojektion im Detail.

Allgemein

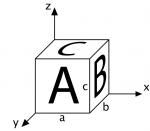
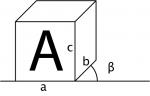
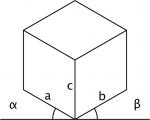
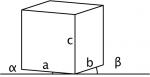
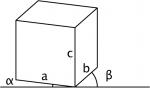
Mit der Parallelprojektion lässt sich der (geometrische) Raum in zwei Dimensionen übersichtlich darstellen. Anhand eines Würfels kann dies gut erklärt werden:

  1. Die Parallelen des Würfels bleiben auf der Zeichenfläche parallel.
  2. Egal ob der Würfel nahe oder fern ist; Die Kanten einer bestimmten Richtung sind immer gleich lang.
  • Im Raum an sich: Ein Würfel ist ein Körper aus 3 X 4 Parralellengruppen, die 6 gleich grossen Quadrate bilden

koordinatenquader_ku-ts
  • Im Bildraum: In der Zeichnung bleiben die Parallelengruppen parallel und die Würfelkanten einer jeweiligen Richtung gleich lang (s1 = s2 oder t1 = t2)

parallel-konstanteverkuerzung_ku-ts

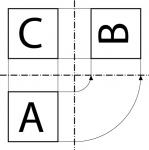
Dreitafelprojektion 

In der Dreitafelprojektion schaut man den Würfel von drei Seiten an (Risse). Die Achsen (Punktstrichlinien) stellen den Wechsel der Blickrichtung dar. Die jeweiligen Quadrate werden dabei nicht verzerrt. Allerdings wirkt der Würfel nicht räumlich. Nebenstehend ist ein Vorschlag zur Anordnung der Risse, die mit den Messlinien aufeinander abgestimmt sind:

tafelprojektion_ku-ts

 

 In der Dreitafelprojektion stehen die drei Hauptprojektionen in Relation zueinander:
  1. Grundriss (A)
  2. Aufriss (C)
  3. Seitenriss (B)

In einer Varianten hiervon könnte auch der Seitenriss (3.) im vierten Quadranten gearde stehen. Auch andere Varianten oder die Einbindung schräger Schnitte sind möglich. Es ist lediglich darauf zu achten, dass die Umklappungen mit den Achsen logisch gezeichnet sind. So können die (feinen) Messlinien genutzt werden.

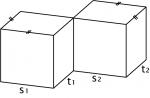
Militär- und Kabinettprojektion

Diese beide Darstellungen ermöglichen eine gute Raumvorstellung. In der Militärprojektion (Grundriss-Schrägbild) wird die Grundfläche und in der Kabinettprojektion (Aufriss-Schrägbild) die Frontfläche nicht verzerrt, was eine zeichnerische Handhabung vereinfacht. Allerdings wirken diese Darstellungen etwas künstlich.
  • Militärprojektion (Grundriss-Schrägbild = Ansicht von oben), Winkel Gamma = 45° oder 30°, hier dimetrisch (sonst in der Regel isometrisch), z.B. zur Darstellung von Stadtplänen

militaer_ku-ts
  • Kabinettprojektion (Aufriss-Schrägbild = Ansicht von vorne), Winkel Beta = 45° oder 30°, in der Regel dimetrisch (hingegen wäre die Kavallierprojektion isometrisch), z.B. zur Darstellung von Fassaden

kabinett_ku-ts

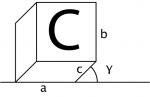Weitere Axonometrien

Weiter gibt es in der Axonometrie Darstellungen, welche die Raumwirkung natürlicher erscheinen lassen. Die Winkel und Verkürzungen entsprechen gegebenen Standards, die mathematisch begründet sind. Axonometrien mit keinen Verkürzungen der drei Richtungen nennt man isometrisch, mit zwei gleichen dimetrisch, mit drei verschiedenen trimetrisch: z.B. Standard-Isometrie oder Trimetrie. Hier werden im Gegensatz zu den obigen Schrägrissen die Quadratflächen verzerrt, was die Handhabung etwas erschwert.
  • Standard-Isometrie (30°/30° und 1:1:1), einfaches Handling mit einem Schablone, allerdings entstehen oft ungünstige Überschneidungen

isometrie_ku-ts
 
  • Trimetrie (5°/18° und 0.9:0.5:1), wirkt noch natürlicher, das zeichnerische Handling ist allerdings etwas schwieriger

 

trimetrie_ku-ts

Freie Parallelprojektion

Die freie Parallelprojektion kann der Di- oder Trimetrie ähneln, wobei die Winkel und Seitenverhältnisse nicht mathematisch vorgegeben sind und den Bedürfnissen entsprechend frei gewählt werden. Somit kann das Objekt ideal erfasst werden, je nach dem, ob mehr Aufsicht Ansicht oder Seitensicht erwüsncht ist. Insbesondere in der Freihandzeichnung lässt sich hier frei und zügig Arbeiten. Diese Perspektive eignet sich etwa zur Entwicklung von Ideen für Möbel, Architekturen, Einrichtugnen etc. Für die weiterführende technische Umsetzung z.B. eines realen Bauvorhabens müsste wohl nach der Ideenfindung eine genormte Axonometrie benutzt werden, wobei dies heute vorwiegend mit CAD-Programmen am Computer passiert.  

 

 dimetrie_ku-ts

Etwas mehr Aufsicht

 

trimetrie_ku-ts

Etwas mehr Ansicht
Details