Die Punktperspektive erlaubt eine Darstellung des dreidimensionalen Raumes auf einer zweidimensionalen Fläche. Im Gegensatz zur Parallelperspektive (eingetlich "Parallelprojektion") wirkt die Punktperspektive wirklichkeitsnäher und eignet sich deshalb besonders für eine täuschend "echte" Wirklichkeit, so z.B. zur Präsentation von Bauvorhaben, phantastischen Räumen oder Ergänzungen in Fotografien. Im Folgenden werden verschiedene Typen der Punktperspektive aufgezeigt, die sich je nach Betrachtungsstandpunkt definieren und somit implizite Bildaussagen enthalten. Für einen kürzeren und anspruchsloseren Zugang siehe den Beitrag Punktperspektive kurz und knapp. (mit Illustrationen des Autors)
Allgemein
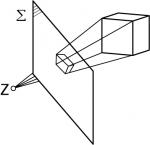
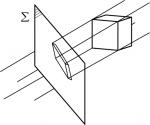
Voraussetzungen: Die Punktperspektive ist wie die Parallelperspektive eine planare Projektion. D.h. die Projektionsebene ist eben, also nicht gekrümmt (sphärisch). Im Gegensatz zur Parallelperspektive sind die Projektionsstrahlen nicht parallel zueinander sondern schneiden sich in einem Zentrum (Z). Dabei wird vom Projektionsgegenstand auf der Projektionsebene ein zweidimensionales Abbild projiziert.
 |
 |
| Punktperspektive | Parallelperspektive |
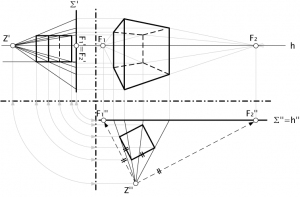
Das Prinzip der Punktperspektive entspricht relativ nahe dem menschlichen Sehen. Das Projektionszentrum (Z) kann dem Betrachterstandpunkt gleichgestellt werden - genauer noch dem menschlichen Auge. So wären die Projektionsstrahlen die Sehstrahlen also das Licht, welches auf das Auge fällt. Der Projektionsgegenstand (hier ein Würfel) entspricht dem Betrachtungsobjekt, dem Sujet. Die Projektionsfläche (Epsilon) einer dazwischen liegenden Fläche zwischen Betrachter und Sujet, bestenfalls einer Zeichenfläche (vgl. Dürerscheibe).
Wenn diese Konstellation auf die Parallelperspektive angewendet wird, wäre dort der Betrachter (Z) unendlich weit entfernt, was in Wirklichkeit nicht möglich ist aber in der Erscheinung der Zeichnung objektiver wirkt. Bei der punktperspektivischen Darstellung erscheinen die Sujets in der Zeichnung jedoch näher, geradezu greifbar und deshalb auch wirklichkeitsnäher.
Auswirkungen: Im Gegensatz zur Parallelperspektive laufen in der punktperspektivischen Darstellung Raumparallelen in einem Punkt zusammen; Sie konvergieren im sogenannten Fluchtpunkt. Falls die Parallelen im Raum ebenfalls parallel zur Projektionsebene liegen, bleiben die Geraden jedoch wie bei der Parallelperspektive auf der Projektionsebene parallel (im unteren Bsp. nur die Vertikalen). Weiter zeigen sich auf der Ebene projizierte Raumdistanzen von weiter Entfernung kürzer als näher stehende aber gleich lange Raumdistanzen derselben Richtung (schwindende Verkürzungen).
Je nach Konstellation von Projektionszentrum (Betrachterstandpunkt), Projektionsebene (Zeichenfläche) und Projektionsgegenstand (Sujet) entwickeln sich verschiedene Typen der Punktperspektive, die sich nach Ihrer Anzahl und Lage der Fluchtpunkte unterscheiden. Die Fluchtpunkte ordnen sich auf dem (theoretischen) Horizont auf, welcher der Augenhöhe entspricht. Um dies aufzuzeigen, geht dieser Beitrag von einem Würfel aus, der jeweils von aussen und von innen (kubischer Innenraum) in den verschiedenen punktperspektivischen Darstellungen visualisiert wird.
Typen der Punktperspektive nach Anzahl der Fluchtpunkte
Einpunkt-Perspektive (Frontalperspektive)
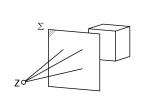
Voraussetzungen: Eine Koordinatenebenen (xy, yz oder zx) steht zur Projektionsebene parallel.
 |
 |
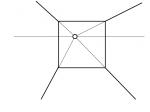 |
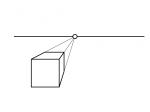
| Voraussetzung | Aussenraum | Innenraum |
Auswirkungen: Alle Geraden einer einzigen Koordinatenrichtung schneiden sich in einem Fluchtpunkt F1, der sich auf dem theoretischen Horizont befindet. Steht der Fluchtpunkt zudem in der horizontalen Mitte der Zeichenfläche, nennt sich dieser Typ Zentralperspektive. Die Geraden der beiden anderen Koordinatenrichtungen bleiben auf der Zeichenfläche parallel - im Idealfall horizontal und vertikal.
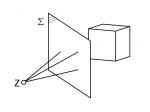
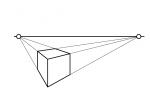
Zweipunkt-Perspektive (Übereckperspektive)
Voraussetzungen: Eine Koordinatenrichtung (x, y oder z) steht zur Projektionsebene parallel.
 |
 |
 |
| Voraussetzung | Aussenraum | Innenraum |
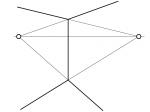
Auswirkungen: Alle Geraden zweier Koordinatenrichtung schneiden sich jeweils in einem Fluchtpunkt F1 bzw. F2, die sich auf dem theoretischen Horizont befinden. Dieser Typ nennt sich auch Übereckperspektive. Die Geraden der dritten Koordinatenrichtung bleiben auf der Zeichenfläche parallel - im Idealfall vertikal.
Um eine unnatürliche Darstellung zu vermeiden, sind die Fluchtpunkte in der Regel jeweils weit auseinander gesetzt bzw. ist als Zeichenfläche ein kleiner Ausschnitt innerhalb der Fluchtpunkte gewählt, was dem menschlichen Gesichtsfeld entspricht. So kann auch ein Fluchtpunkt im Bild sein und der zweite weit ausserhalb der Zeichenfläche.
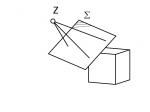
Dreipunkt-Perspektive
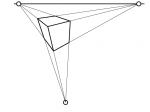
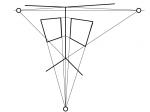
Voraussetzungen: Keine Koordinatenrichtung (x, y oder z) steht zur Projektionsebene parallel.
 |
 |
 |
| Voraussetzung | Aussenraum | Innenraum |
Auswirkungen: Die Geraden aller drei Koordinatenrichtung schneiden sich jeweils in einem Fluchtpunkt F1, F2 bzw. F3, wovon sich zwei Fluchtpunkte auf dem theoretischen Horizont befinden. Keine Geraden bleiben auf der Zeichenfläche parallel.
Um eine unnatürliche Darstellung zu vermeiden, wird auch hier - wie bei der Zweipunktpwerseptkvie - als Zeichenfläche ein kleiner Ausschnitt innerhalb der Fluchtpunkte gewählt, was dem menschlichen Gesichtsfeld entspricht.
Mehrpunkt-Perspektive
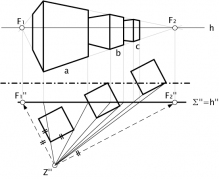
Eine Mehrpunkt-Perspektive ist mit der Ausgangslage eines einzigen Würfels (Koordinatenquaders) nicht möglich, da die Kanten des Quaders lediglich drei Richtungen aufweisen (x,y,z) und somit nicht mehr als drei Fluchtpunkte entstehen können. Wird nun aber zusätzlich ein zweiter Quader dazugestellt und leicht gedreht, entstehen je nach Anzahl der neuen Richtungen weitere Fluchtpunkte (oder unter bestimmten Bedingungen neue Parallelenrichtungen). Denn wechselt eine Gerade Ihren Richtung, so verschiebt sich dem entsprechend auch Ihr Fluchtpunkt. Unter Mehrpunkt-Perspektive versteht sich also, die Projektion von Raumgegenständen, die mehr als drei Richtungen aufweisen. Die Mehrpunkt-Perspektive ist somit in dieser Zusammenstellung konsequenterweise fehl am Platz.
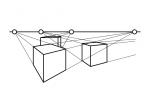 |
| Verschieden gerichtete Würfel |
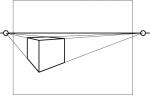
Variation der Punktperspektive durch die Höhe des Horizontes
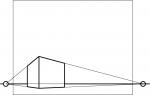
Voraussetzung: Der Horizont befindet sich in der Normalperspektive durch den ausgewählten Bildausschnitt in Etwa im mittleren Drittel, in der Froschperspektive am unteren Bildrand und in der Vogelperspektive am oberen Bildrand.
Auswirkung: Durch die Wahl der Höhe des Horizontes im Bild kann der Blickwinkel des Betrachters und somit die Bildwirkung gesteuert werden (von unten hoch schauen = Froschperspektive / von oben hinunter schauen = Vogelperspektive).
 |
 |
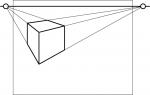 |
| Froschperspektive | Normalperspektive | Vogelperspektive |
Anmerkungen
Zu Beginn des Beitrages wurde darauf verwiesen, dass die Punktperspektive dem menschlichen Sehen nahe kommt. Damit in der punktperspektivischen Darstellung die Projektion jedoch tatsächlich dem projizierten Gegenstand entspricht, müssten bei der Betrachtung konsequenterweise zwei Einschränkungen gemacht werden: Erstens dürfte die Zeichenfläche nur mit einem Auge (monokulares Sehen) betrachtet werden. Zweitens müsste das Bild von einem eindeutig definierten Standpunkt zur Zeichenfläche (dem Projektionszentrum) betrachtet werden.
Allerdings haben sich unsere Sehgewohnheiten durch unsere Bildkultur so konventionalisiert, dass wir ein Bild auch bei einer schrägen Betrachtung mit zwei Augen interpretieren können und als wirklichkeitsnahe empfinden.
Dem gegenüber steht die Stereografie, die tatsächlich auf dem zweiäugigen Sehen beruht (binokulares Sehen). Jedes Auge erhält durch je ein Bild eine leicht andere, räumlich verschobene Bildinformation. Bei gewissen Verfahren wird zudem der Betrachtungsstandpunkt vom jeweiligen Auge zum Bild fest definiert. Die erzeugte Raumtiefe kommt somit der Betrachtung der Wirklichkeit überraschend nahe. Doch durch weitere Gesetzt der Optik wird man aber hier bemerken, dass dies lediglich eine Annäherung an die Wirklichkeit ist. Auch wenn nun alle Aspekte der Optik, Textur, Bewegung, Audio und weitere sensuelle Schranken geklärt sind, wie stände es dann mit der Wirklichkeitsnähe im Verhältnis zur Wirklichkeit? Würde Walter Benjamin mit seinem Aufsatz zum Verlust der Aura bei technischen Reproduktionen weiterhelfen? Oder müsste man noch weiter gehen und das Verhältnis von Mensch und Umwelt klären?